Robust and Constrained Multi-Agent Reinforcement Learning for Autonomous Mobility-on-Demand Systems

We are happly to introduce our recent publication on 2023 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS):

“A Robust and Constrained Multi-Agent Reinforcement Learning Electric Vehicle Rebalancing Method in AMoD Systems”

  1. IROS 23
    A Robust and Constrained Multi-Agent Reinforcement Learning Electric Vehicle Rebalancing Method in AMoD Systems
    Sihong He, Yue Wang, Shuo Han, and 2 more authors
    In 2023 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 2023
    Bib HTML PDF Website

Abstract

Electric vehicles (EVs) play critical roles in autonomous mobility-on-demand (AMoD) systems, but their unique charging patterns increase the model uncer- tainties in AMoD systems (e.g. state transition probability). Since there usually exists a mismatch between the training and test (true) environments, incorporating model uncertainty into system design is of critical importance in real-world applications. However, model uncertainties have not been considered explicitly in EV AMoD system rebalancing by existing literature yet and remain an urgent and challenging task. In this work, we design a robust and constrained multi-agent reinforcement learning (MARL) framework with transition kernel uncertainty for the EV rebalancing and charging problem. We then propose a robust and constrained MARL algorithm (ROCOMA) that trains a robust EV rebalancing policy to balance the supply-demand ratio and the charging utilization rate across the whole city under state transition uncertainty. Experiments show that the ROCOMA can learn an effective and robust rebalancing policy. It outperforms non-robust MARL methods when there are model uncertainties. It increases the system fairness by 19.6% and decreases the rebalancing costs by 75.8%.

What is an Autonomous Mobility-on-Demand System?

Autonomous mobility-on-demand (AMoD) system is one of the most promising energy-efficient transportation solutions as it provides people with one-way rides from their origins to destinations by using self-driving vehicles. Electric vehicles (EVs) are being adopted worldwide for environmental and economical benefits, and AMoD systems embrace this trend without exception.

Motivations

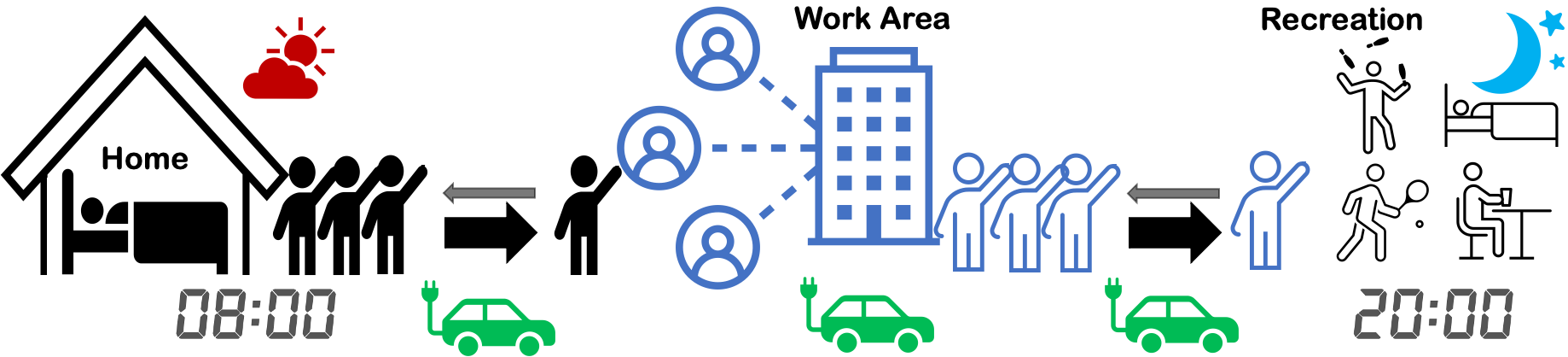
However, the trips in AMoD systems sporadically appear, and the origins and destinations are asymmetrically distributed. As shown above, unbalanced demand and supply happen several times a day. For example, at morning peak, there are more commutes from the residential area to the work zone. While at evening peak, there are more needs to leave the work area to recreational area or home. Such spatial-temporal nature of urban mobility motivates researchers to study vehicle rebalancing methods, i.e. redistribution of vacant EVs to areas of high demand and assigning low-battery EVs to charging stations.

In real-world AMoD systems, the simulation-to-reality gap remains challenging for vehicle rebalancing solutions calculated based on simulators, since there usually exists a model mismatch between the simulator (training environment) and the real world (test environment). For example, in the follow figure, the model mismatch between the simulator and the real world degrades the performance of vehicle rebalancing methods. The red EV chooses to go to the blue region at time t and thinks it can pick up a passenger at time t + 1 according to the simulator model. However, in the real world, at time t + 1, the red EV gets no passengers in the blue region and a passenger gets no cars in the green region.

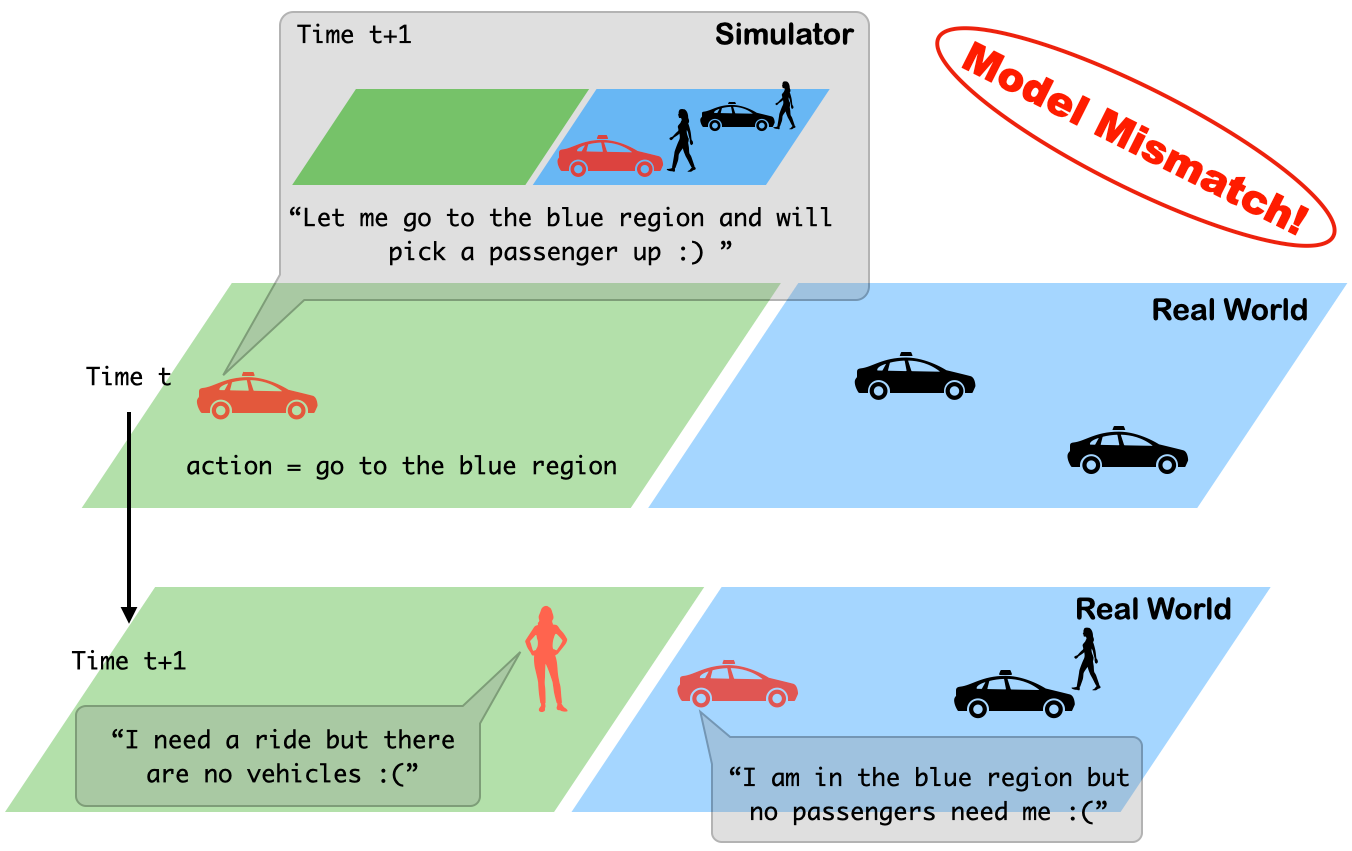
Moreover, in real-world applications, the vehicle rebalancing decisions should satisfy specific constraints such as providing fair mobility service in different regions. Despite model-based methods considering prediction errors in mobility demand or vehicle supply, how to calculate policies that satisfy the constraints and optimize the objectives under model uncertainty of the dynamic state transition remains largely unexplored for AMoD rebalancing algorithms. In this work, to address the simulation-to-reality gap and calculate solutions that satisfy the constraints, we propose a robust and constrained multi-agent reinforcement learning (MARL) framework for EV AMoD system rebalancing.

Contributions

  • (1) To the best of our knowledge, this work is the first to formulate EV AMoD system vehicle rebalancing as a robust and constrained multi-agent reinforcement learning problem under model uncertainty. Via a proper design of the state, action, reward, cost constraints, and uncertainty set, we set our goal as minimizing the rebalancing cost while balancing the city’s charging utilization and service quality, under model uncertainty.

  • (2) We design a robust and constrained MARL algorithm (ROCOMA) to efficiently train robust policies. The proposed algorithm adopts the centralized training and decentralized execution (CTDE) framework. We also develop the robust natural policy gradient (RNPG) in MARL for the first time.

  • (3) We run experiments based on real-world E-taxi system data. We show that our proposed algorithm performs better in terms of reward and fairness, which are increased by 19.6%, and 75.8%, respectively, compared with a non-robust MARL-based method when model uncertainty is present.

Goal

The goal of our robust and constrained MARL EV rebalancing problem is to find an optimal joint policy \(\pi^*\) that maximizes the worst-case expected value function subject to constraints on the worst-case expected cost: \begin{align} \max_{\pi} \mathbb{E}_{s \sim \rho} [ v^{\pi}_{r}(s) ] \text{ s.t. } \mathbb{E}_{s \sim \rho} [ v^{\pi}_c(s) ] \geq d \end{align} We define \( v^{\pi_\theta}_{tp} (\rho)= \mathbb{E}_{s\sim\rho}[v^{\pi_\theta}_{tp} (s)] \), \({tp} \in \{r,c\}\). We then consider policies \(\pi(\cdot | \theta)\) parameterized by \(\theta\) and consider the following equivalent max-min problem based on the Lagrangian: \begin{align} \label{prob_roco_cmarl} \max_{\theta} \min_{\lambda \geq 0} J(\theta, \lambda) := v^{\pi_\theta}_r(\rho) + \lambda (v^{\pi_\theta}_c(\rho) - d), \end{align} For more information of how the value functions, policies are defined, please check the paper.

Algorithm

We propose a robust and constrained MARL (ROCOMA) algorithm to solve the AMoD balancing problem and train robust policies. The proposed algorithm is shown in Algorithm 1. It adopts the centralized training and decentralized execution (CTDE) framework, which enables us to train agents in the simulator using global information but executes well-trained policies in a decentralized manner in the real world. Specifically, we use centralized critic networks to approximate the value functions and decentralized actor networks to represent policies. Besides, we develop a robust natural policy gradient (RNPG) descent ascent to update actor networks and the Lagrange multiplier.

Experimental Results

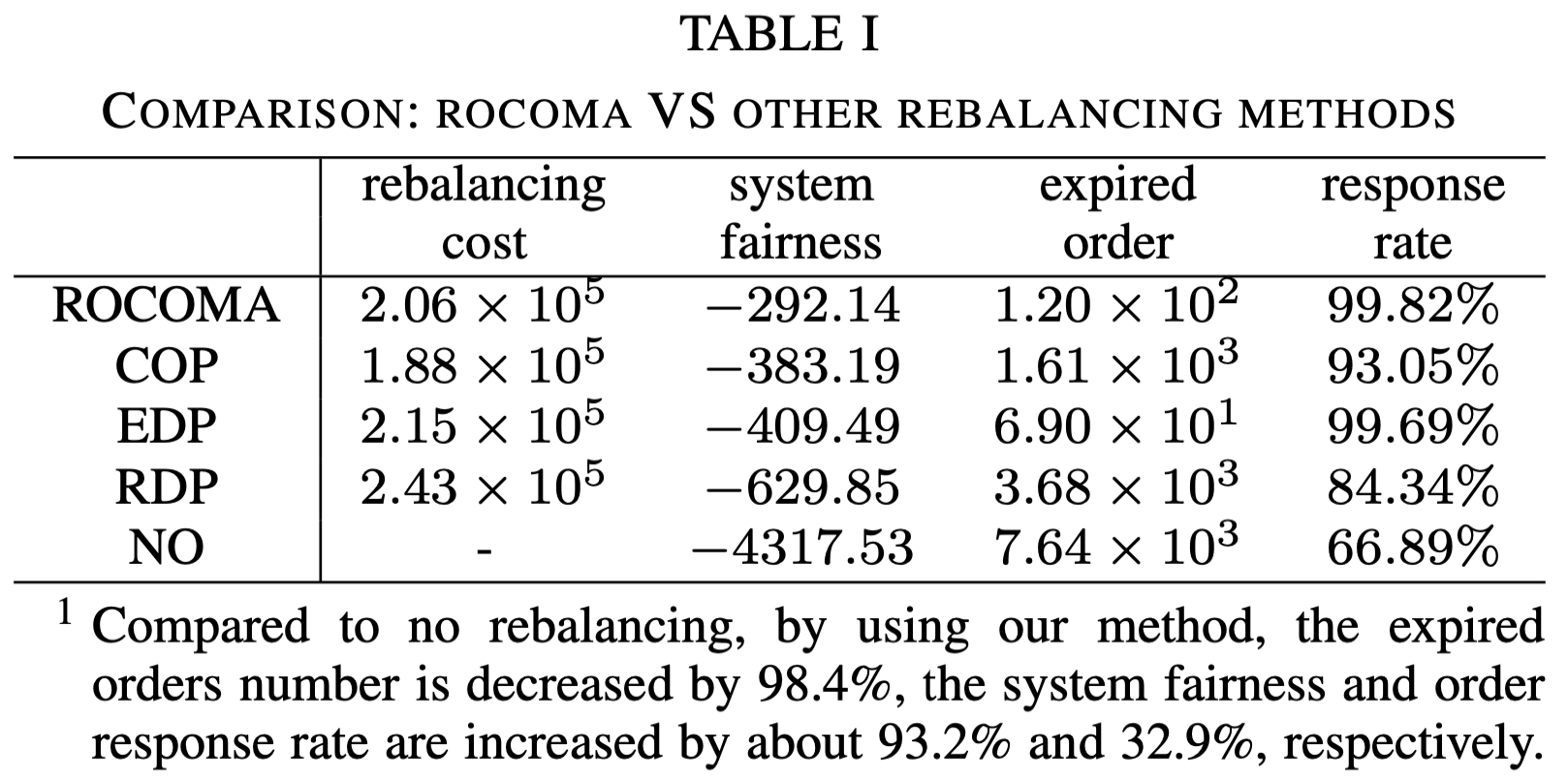
In Table I, compared to the no rebalancing scenario, ROCOMA is effective in rebalancing AMoD systems in terms of fairness, expired orders and response rate. Specifically, ROCOMA policy decreases the number of expired orders by 98.4%, increases the system fairness and order response rate by about 93.2% and 32.9%, re- spectively. Besides, ROCOMA achieves a higher system fairness and order response rate using less rebalancing cost than EDP and RDP.

  • No: No reblancing

  • Constrained optimization policy (COP): The optimization goal is to minimize the rebalancing cost under the fairness constraints. The fairness limit is the same as that used in ROCOMA. The dynamic models are calculated from the same data sets used in simulator construction.

  • Equally distributed policy (EDP): EVs are assigned to their current and adjacent regions using equal probability.

  • Randomly distributed policy (RDP): EVs are randomly distributed to their current and adjacent regions.

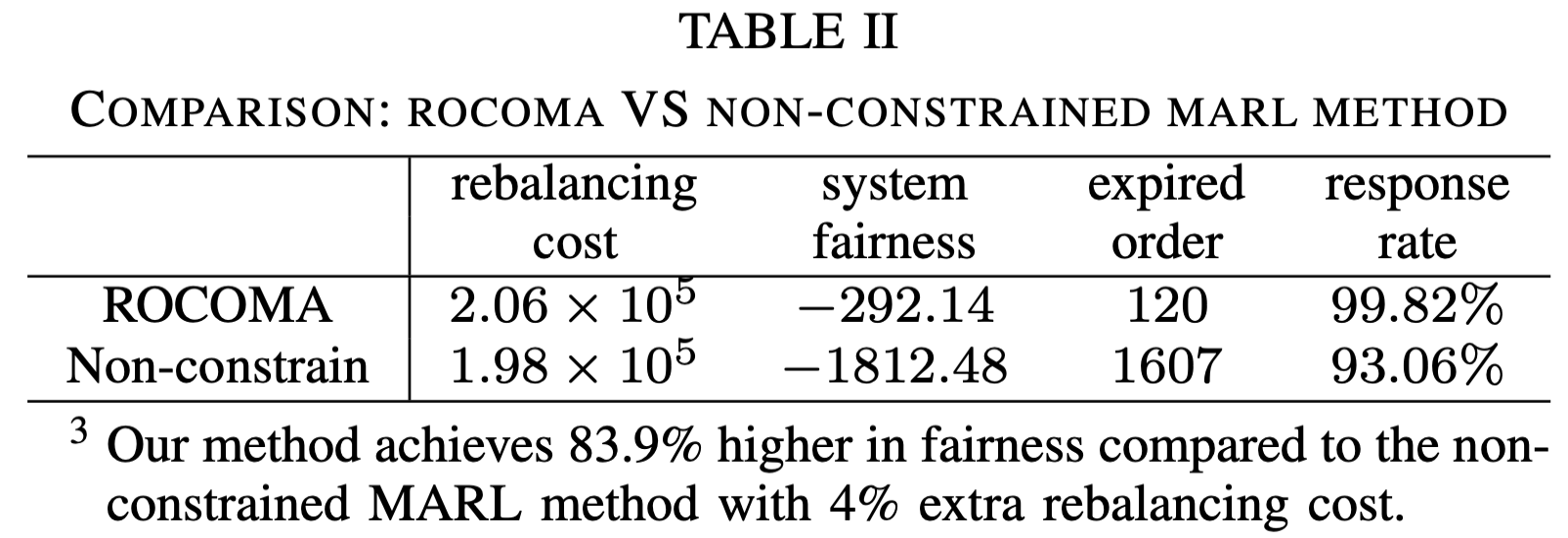
In Table II, ROCOMA achieves 83.9% higher in fairness compared to the non-constrained MARL algorithm with just 4% extra rebalancing cost. Without the fairness constraint design, the non-constrained MARL method falls into a pit that sacrifices fairness to achieve a lower rebalancing cost since its objective is a weighted sum of them. It would take a lot of effort to tune the hyper-parameter to find a policy that performs well in both rebalancing cost and fairness. The constrained MARL design of ROCOMA avoids such extra tuning efforts.
  • Non-constrained MARL method: Instead of considering fairness constraints in MARL, the reward is designed as a weighted sum of negative rebalancing cost and system fairness. The coefficient is 1. And model uncertainty is considered.

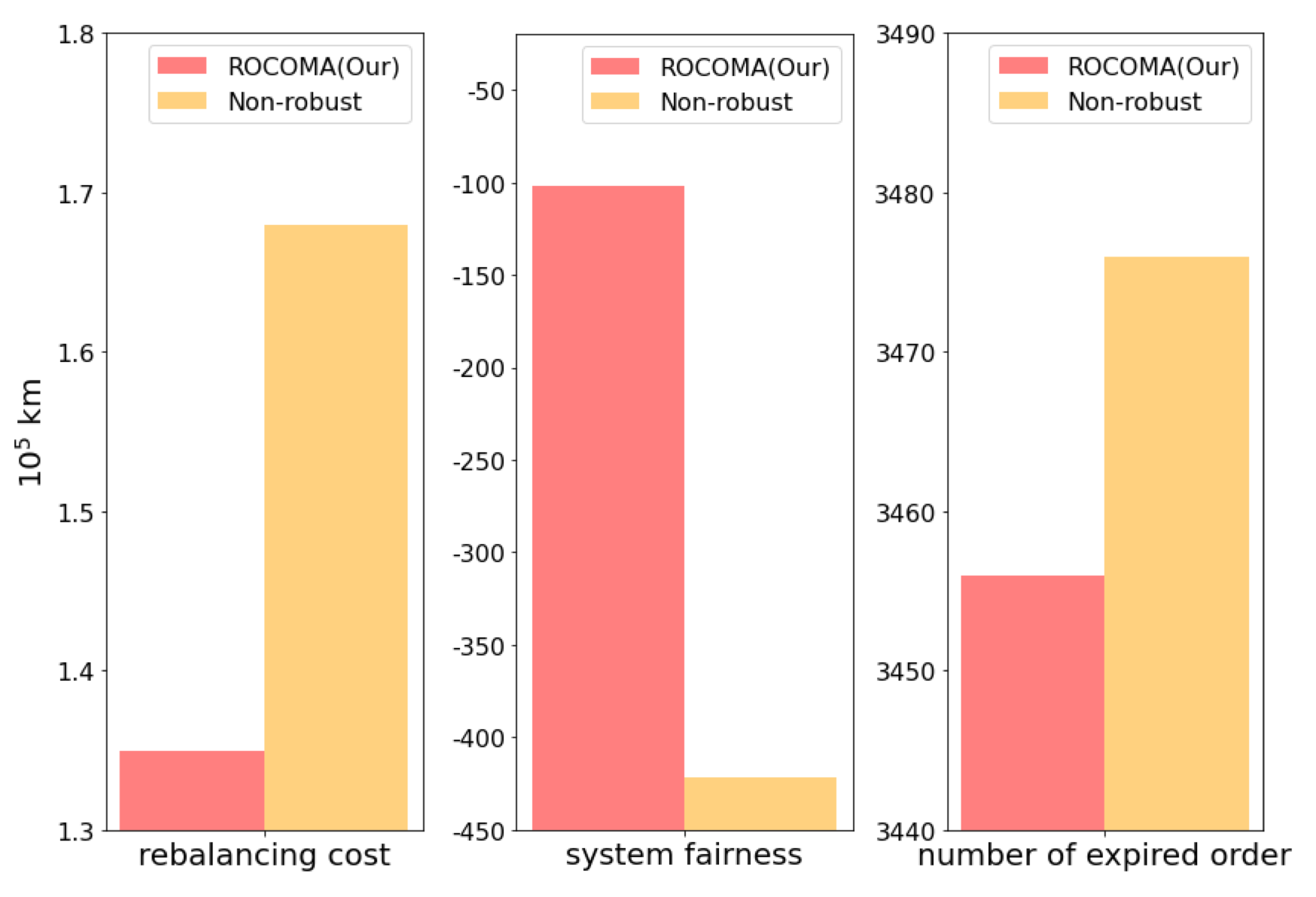
In this figure, we test well-trained robust and non- robust methods in a testing environment (different from the training environment) to show the robustness of the ROCOMA policy. We can see ROCOMA policy achieves better performance in terms of all metrics. Specifically, ROCOMA decreases the rebalancing cost and increases the system fairness by about 19.6% and 75.8% , respectively, when model uncertainty exists, compared to the non-robust method.
  • Non-robust MARL method: The model uncertainty is not considered but the fairness constraint is considered in MARL. They use the same network structures and other hyper-parameters as that in ROCOMA.

You may also be interested in our related publications on IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), IEEE Transactions on Intelligent Transportation Systems (TITS) and ACM Transactions on Cyber-Physical Systems (TCPS):

  1. IROS 23
    Robust electric vehicle balancing of autonomous mobility-on-demand system: A multi-agent reinforcement learning approach
    Sihong He, Shuo Han, and Fei Miao
    In 2023 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 2023
    Bib PDF
  1. TITS
    Data-Driven Distributionally Robust Electric Vehicle Balancing for Autonomous Mobility-on-Demand Systems Under Demand and Supply Uncertainties
    Sihong He, Zhili Zhang, Shuo Han, and 5 more authors
    IEEE Transactions on Intelligent Transportation Systems, 2023
    Bib HTML PDF Website
  1. TCPS
    Data-driven distributionally robust optimization for vehicle balancing of mobility-on-demand systems
    Fei Miao, Sihong He, Lynn Pepin, and 5 more authors
    ACM Transactions on Cyber-Physical Systems, 2021
    Bib HTML